Wer im Umfeld von maschinellem Lernen, künstlicher Intelligenz oder Data Science unterwegs ist, stößt schnell auf den Begriff „Neuronales Netz“ oder „Deep Learning“. Diese Technologien scheinen das Patentrezept für alle Aufgaben zu sein, die mit KI zu tun haben, und sind die treibende Kraft hinter Computer Vision, Natural Language Processing, Spracherkennung und vielem mehr. Für Menschen, die keine Experten auf diesem Gebiet sind, wirken neuronale Netze oder Deep Learning jedoch eher wie eine obskure Superkraft, die sehr komplexe Aufgaben zu lösen vermag.
Um das Feld der neuronalen Netze für alle Arten von Praktikern zugänglich zu machen, veröffentlichen wir in den kommenden Wochen eine umfassende Reihe von Blogbeiträgen zu diesem Thema.
Mit der Blogreihe möchten wir neuronale Netze und ihre Erweiterungen verständlicher machen. Wir werden zeigen, dass die grundlegenden Prinzipien neuronaler Netze auf einfachen mathematischen Berechnungen basieren, die jeder verstehen kann, der über grundlegende Kenntnisse der linearen Algebra oder Integralrechnung verfügt. Die Kenntnis der Grundlagen erleichtert das Verständnis der komplexeren Anwendungsfälle im weiteren Verlauf der Reihe.
In unserem ersten Beitrag unternehmen wir eine Reise in die Geschichte der neuronalen Netze. Es folgen Artikel über die Grundlagen neuronaler Netze, angefangen bei einfachen Konzepten, und darauf aufbauend ergänzt um komplexere Erweiterungen. Wir hoffen, dass diese Serie Ihnen einen besseren Überblick über dieses allgegenwärtige Thema im #ageofdata vermittelt.
Eine kurze Geschichte der neuronalen Netze
Nachahmung der Funktionsweise des Gehirns
In diesem Beitrag sehen wir uns an, wie die Idee der neuronalen Netze entstanden ist und wie die Vordenker der künstlichen Intelligenz auf dieses Konzept kamen. Der Erfolg bei der Nachbildung einiger grundlegender Funktionsweisen des Gehirns durch neuronale Netze geht auf eine Reihe von Konzepten aus so unterschiedlichen Bereichen wie Philosophie, Mathematik, Wirtschaft, Neurowissenschaften, Psychologie, Steuerungstheorie, Computertechnik und in gewissem Maße auch Linguistik zurück. Man muss zunächst wissen, dass die Geschichte der sogenannten neuronalen Netze nur im Kontext eines größeren Ganzen richtig verstanden werden kann: des Strebens nach intelligenten Systemen. Schon eine Definition für Intelligenz zu finden, kann eine ziemliche Herausforderung darstellen – zumal wir schon seit der Antike versuchen, uns selbst und die innerste Funktionsweise unseres Bewusstseins zu beschreiben.
Es ist eine Reise durch die Zeit, die Wissenschaft und unser Gehirn. Sie führt Sie von der Art und Weise, wie Gehirne Entscheidungen treffen, über deren Aufbau auf zellularer Ebene und Interaktionen bis hin zu der Frage, was es bedeutet, wenn ein Computer ein Gehirn nachahmt. In diesem Artikel soll die Geschichte der Entstehung neuronaler Netze deutlich werden. Das Ziel ist, das Konzept der neuronalen Netze zu entmystifizieren und zugänglicher zu machen. Erste Station: Aristoteles.
Betreiben wir Philosophie
Die Philosophie befasst sich intensiv mit der komplizierten Aufgabe, die Funktionsweise unseres Bewusstseins zu beschreiben. Aristoteles wird oft als Urheber der Vorstellung bezeichnet, dass wir die Teile des Gehirns, die uns Schlussfolgerungen anhand eines Satzes von Regeln ziehen lassen, erfassen und formalisieren können. Diese sogenannten Syllogismen sind wahrscheinlich das erste Konzept eines regelbasierten Datensatzes, der als Eingabe für eine schlussfolgernde Einheit dient.
Alle Menschen sind sterblich. – Prämisse (Voraussetzung)
Alle Griechen sind Menschen. – Prämisse (Voraussetzung)
Alle Griechen sind sterblich. – Konklusion (Schlussfolgerung)
Beispiel für einen Syllogismus nach der Definition von Aristoteles
Wenn wir das wissen, können wir davon ausgehen, dass Algorithmen, die auf Computern ausgeführt werden, das gleiche könnten – denn was ist ein Algorithmus anderes als eine Reihe von Anweisungen in einer bestimmten Reihenfolge? Dies ist ein ideales Prinzip, um Schlussfolgerungen zu ziehen, die auf Regeln als Eingabe basieren. Ein paar Jahrhunderte später trugen die Werke von Thomas Hobbes und René Descartes zur Formalisierung des Denkens bei: Argumentation, Kausalität und Rationalität wurden Teil von Analysis und Rechnen. David Hume kam ins Spiel, indem er die Verbindung zwischen Wissen und wiederholter Exposition darlegte. Damit war die Grundlage für die Darstellung von Intelligenz durch eine Maschine gelegt.
Das Gehirn
So wie ein Rezept der Schlüssel zum erfolgreichen Backen eines Kuchens ist, ist das Wissen darum, wie unser Gehirn Gedanken erzeugt, von entscheidender Bedeutung dafür, es in leblosen Schaltkreisen in einem Computer zu simulieren.
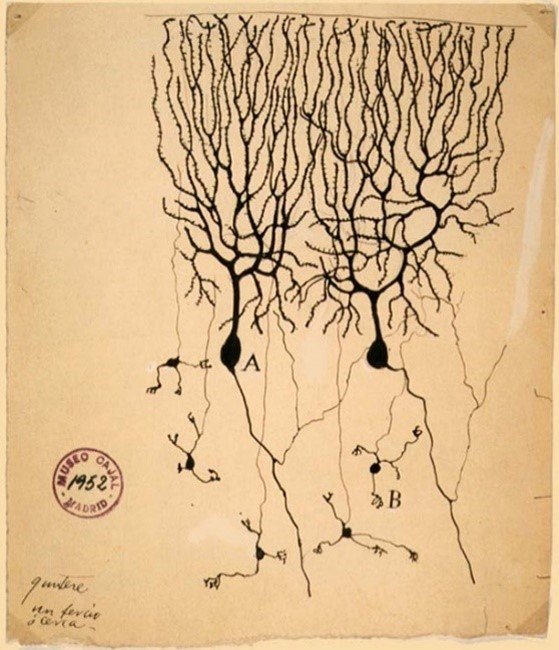
Unser Hirngewebe besteht aus einer Vernetzung von Nervenzellen: Unser Nervensystem besteht aus Hunderten Milliarden Nervenzellen, die über sogenannte Synapsen miteinander verbunden sind, die Signale zwischen den Zellen übertragen. Diese Auffassung von der Struktur des Gehirns wurde erstmals Ende des 19. Jahrhunderts von Santiago Ramón y Cajal vorgestellt. Cajal hatte bei Experimenten mit Gewebeproben festgestellt, dass, eine Reaktion zu beobachten ist, wenn man das Gewebe in eine Silbernitratlösung eintaucht. Dadurch wurde vorher Unsichtbares sichtbar: Linien zeichnen sich ab, die die Nervenzellen und das komplexe Netz der Verbindungen zwischen ihnen darstellen. 1906 erhielt Cajal den Nobelpreis für Physiologie oder Medizin (die Kategorie umfasst beide Disziplinen, auch wenn sie oft als Medizinnobelpreis abgekürzt wird) für seine Arbeit über die Struktur des Nervensystems, zusammen mit Camillo Colgi, der die Färbemethode erfunden hatte.
Cajals Anwendung von Colgis Färbemethode zeigt die Neuronen und ihre Verflechtung
Quelle: Wikipedia
Dieser Fortschritt im Verständnis der Funktionsweise des Gehirns war von grundlegender Bedeutung: Es war bereits bekannt, dass man Information mithilfe elektrischer Signale über Entfernungen übertragen kann, zum Beispiel durch das Ein- und Ausschalten eines elektrischen Stroms. Außerdem hatte man bereits die Entdeckung gemacht, dass elektrische Ströme, die durch Nerven pulsieren, auch für die Kommunikation innerhalb organischer Lebensformen verantwortlich sind. Die Entdeckung von Cajal und Colgi, dass die Hirnsubstanz aus speziellen, miteinander verbundenen Neuronen besteht, führte zu der Schlussfolgerung, dass diese auch auf die gleiche Weise kommunizieren: durch die Übertragung und Verarbeitung elektrischer Signale. Schauen wir uns ein solches Neuron, die Nervenzelle des Gehirns, einmal an:
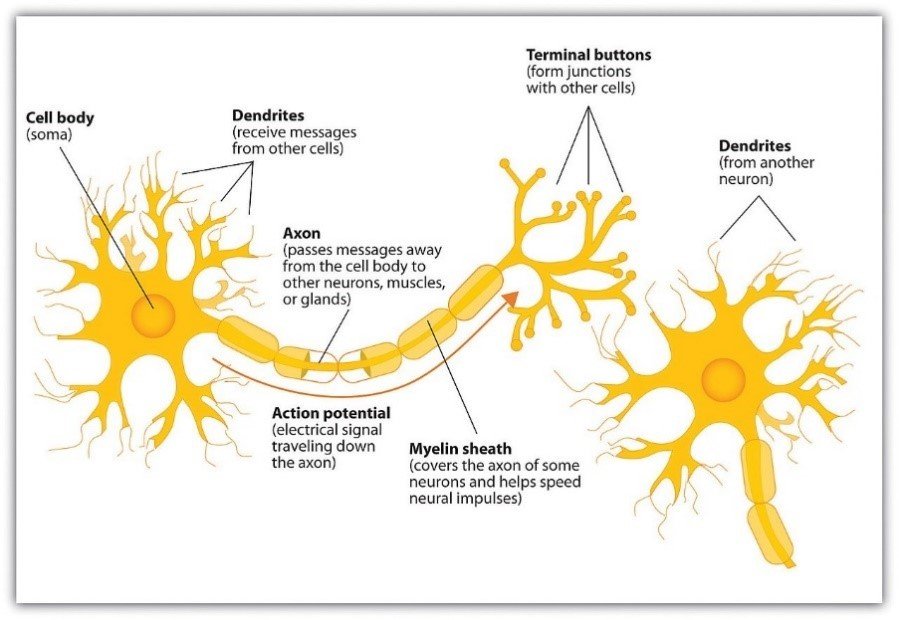
Schematische Darstellung eines Neurons und seiner Bestandteile.
Quelle: Wikipedia
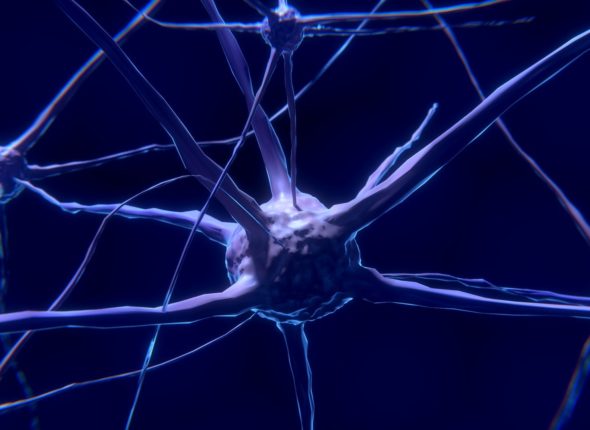
Neuronen und ihre Verbindungen in der Hirnbildgebung
Quelle: Wikipedia
Ein Neuron besteht aus einem Körper (Soma) und Verästelungen, die wie ausgefranste Verlängerungen des Zellkörpers aussehen. Wir können zwischen zwei Arten dieser Verästelungen unterscheiden: Dendriten, von denen ein Neuron mehrere hat, und das Axon, das jede Zelle nur einfach hat. Die Dendriten sind für den Empfang von Signalen von anderen Neuronen zuständig, während das Axon (über seine Endknöpfchen) ein Ausgangssignal an die Neuronen sendet, mit denen es verbunden ist. Zusammen mit dem synaptischen Spalt, der Sender- und Empfängerzellen trennt, bilden die Dendriten der Empfängerzelle und die Endknöpfchen der Senderzelle die Synapse.
Dieses komplexe Netzwerk – aus Empfang von Eingangssignalen über die Dendriten und der Erzeugung eines Ausgangssignals über das Axon – bildet gemeinsam die Art und Weise, wie Informationen in Form von elektrischen Impulsen das Gehirn durchlaufen. Es gibt eine gewisse Systematik, warum und wie Neuronen diese Verbindungen bilden; nicht jedes Neuron ist mit jedem anderen Neuron verbunden. Wenn wir die sogenannte „graue Substanz“ in der Hirnbildgebung betrachten, beschreiben wir im Wesentlichen die Zellkörper der Neuronen. Wenn wir nun darüber sprechen, wie diese Vorstellung in einem nicht-organischen, emulierten Kontext auf einem Computer umgesetzt werden kann, müssen wir im Hinterkopf behalten, dass die neuronalen Netze, die wir in der Computertechnik einsetzen, eine grobe (wenn auch schöne) Vereinfachung dessen sind, was in unseren Gehirnen vor sich geht.
Das Schwellenwertelement – Abbildung einer einfachen Logik
Die Forscher hatten schon immer ein großes Interesse daran, unser Gehirn und uns selbst zu kopieren und zu imitieren und den Anspruch zu erheben, beide zu verstehen. Einen wichtigen Schritt auf dem Weg zu einem Gebiet, das erst später als „Künstliche Intelligenz“ bezeichnet werden würde, machten McCulloch und Pitts, als sie Anfang der 1940er Jahre das erste künstliche Neuron schufen: das Schwellenwertelement (Threshold Logic Unit, TLU). Es wurde speziell entwickelt, um die neuronale Vernetzung in unserem Gehirn nachzubilden. Wir wissen bereits, dass Neuronen elektrische Eingangssignale von anderen Neuronen empfangen, die mit ihren Dendriten verbunden sind. Was (im Anschluss daran) im Inneren des Neurons geschieht, ist eine Art Aktivierung: Neuronen feuern nicht ständig, und sie senden auch nicht immer über ihre Axone ein Signal an ihre Nachbarneuronen. Diese Art von Aktivierung – wann ein Neuron feuert und wann nicht – hängt stark von der Eingabe ab. In diesem Zusammenhang erlangte eine Faustregel Berühmtheit: „Neurons that fire together, wire together“, etwas weniger griffig auf Deutsch: Neuronen, die zusammen feuern, vernetzen sich auch miteinander. Der Grad der Aktivierung („feuern“) oder umgekehrt der Grad der Hemmung („nicht feuern“) hängt von der Eingabe ab, die die Neuronen von anderen Neuronen erhalten, die mit ihnen verbunden sind. Dies ähnelt stark dem, was in einem Schaltkreis passiert: ein oder aus, null oder eins, Energie fließt oder nicht.
Wenn wir die Kommunikation zwischen Neuronen in dieser Weise verstehen, können wir bereits über die Implementierung einer einfachen Logik nachdenken: Ein Neuron, das feuert, bedeutet „wahr“, ein Neuron, das ruht, bedeutet „falsch“. Um diese Vorstellung nun etwas stärker zu konzeptionalisieren: Wie kommen wir zu einem logischen „wahr“ und „falsch“, wenn es mehrere Eingaben gibt? Einfacher ausgedrückt: Wie kommen wir zu „feuern“ oder „nicht feuern“, wenn ein Neuron von einer Handvoll vorgeschalteter Neuronen Signale erhält und von anderen nur Stille?
Die Forscher wandelten die von ihnen modellierten Neuronen in Inhibitoren einer Schwellenwertfunktion um. Das bedeutet, dass jedes Neuron einen Schwellenwert hat, von dem abhängt, ob es feuert: Angenommen, dieser Schwellenwert ist 1, dann muss die Summe der Eingaben des Neurons 1 erreichen, damit es feuert. Sonst bleibt es still. Indem wir Schwellenwerte und Signalstärke kombinieren und festlegen, können wir Logik modellieren.
Nehmen wir zum Beispiel an, wir haben einen Schwellenwert von 2 und zwei Eingaben mit dem Wert 1: Dann erreicht die Summe der beiden Eingaben den Schwellenwert, und das Neuron feuert. Dies entspricht dem logischen UND. Wenn wir den Schwellenwert auf 1 setzen und die Eingaben gleich lassen, haben wir eine ODER-Verknüpfung, denn die Eingabe von jedem der vorgeschalteten Neuronen reicht aus, um das Feuern auszulösen. Kurz gesagt: Jedes Neuron erhält ein Eingangssignal von vorgeschalteten Neuronen, mit denen es verbunden ist. Diese Eingaben addieren sich auf, und die entstandene Summe durchläuft eine Aktivierungsfunktion als Argument. Auf diese Weise können wir eine ähnliche Logik wie bei elektronischen Schaltkreisen simulieren, denn die Art und Weise, wie elektrische Signale in Schaltkreisen weitergeleitet werden, ähnelt in gewisser Weise der Funktionsweise der Synapsen unserer Nervenzellen – sehr abstrakt betrachtet.
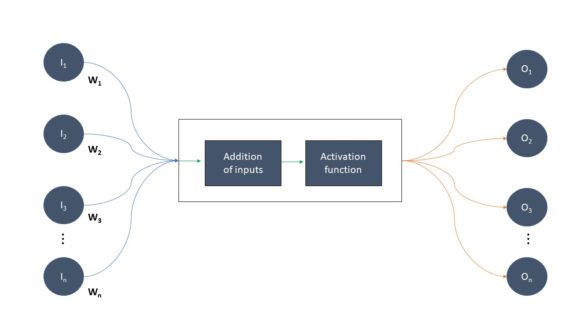
Erinnern Sie sich an die Erkenntnis, dass Neuronen, die zusammen feuern, sich auch miteinander vernetzen? Je öfter Neuronen zusammen feuern, desto stärker wird ihre Verbindung. Wir simulieren diese Verbindung, indem wir die Ausgabe eines bestimmten Neurons mit einem Gewicht versehen, das davon abhängt, mit welchem nachgeschalteten Neuron es kommuniziert – und wie oft sie in der Vergangenheit kommuniziert haben. Je mehr Kommunikation stattgefunden hat, desto höher ist logischerweise das Gewicht. Daraus ergibt sich die folgende schematische Darstellung eines künstlichen Neurons:
Schematische Darstellung eines künstlichen Neurons
Das einschichtige Perzeptron
Diese Simulation eines Neurons eignet sich besonders gut für eine häufig gestellte Frage im Bereich des maschinellen Lernens und der künstlichen Intelligenz: Gehört ein Input einer bestimmten Klasse an? Ein Beispiel, um es einfach auszudrücken: Enthält ein Bild eine bestimmte Form oder Farbe? Wir können eine Reihe von Eingaben, zum Beispiel gerade Vektoren, nehmen und ihre Summierung (oder das Punktprodukt bei Vektoren) in eine einfache binäre, auf Ja/Nein basierende Aktivierungsfunktion einspeisen. Das Konzept des Perzeptrons entstand aus diesem Gedanken, den Frank Rosenblatt Ende der 1950er Jahre vorgestellt hatte. Das Rosenblatt-Perzeptron beginnt mit den Werten für die Gewichte und die Aktivierungsfunktion und konfrontiert dann dieses künstliche Neuron mit der sogenannten Trainingsmenge. Das heißt, wir legen ihm eine Reihe von Daten vor, bei denen wir etwas über die Informationen wissen, die wir vorhersagen wollen.
Nehmen wir an, unser Neuron soll später ableiten oder erraten, ob es ein Bild eines Dreiecks gesehen hat oder nicht. Also werden wir die Ausgabe für jedes Beispiel eines Bildes, das Formen enthält, wiederholt berechnen. Wir können dies tun, indem wir jedes Bild in die Farb- oder Sättigungswerte seiner Pixel zerlegen. Diese Pixelwerte werden als Eingaben in unser Netzwerk eingespeist, und ihre gewichtete Summe bestimmt, ob die Aktivierungsfunktion feuert oder nicht, oder anders ausgedrückt, ob das Bild ein Dreieck enthält oder nicht.
Was aber, wenn die Ausgabe unserer Funktion falsch ist? Von unserem Beispiel ausgehend, lautet die Lernregel für ein neuronales Netz einfach ausgedrückt: Nimm jedes Bild und berechne seine Ausgabe. Wenn die berechnete Ausgabe falsch ist, werden die den Eingaben zugeordneten Gewichte angepasst. Wenn jedoch die Ausgabe korrekt ist, werden die Gewichte nicht verändert. Wenn die wahre Ausgabe 1 (enthält ein Dreieck), die vorhergesagte Ausgabe aber 0 (kein Dreieck) ist, müssen die Gewichte erhöht werden, um die Wahrscheinlichkeit zu erhöhen, dass der Schwellenwert überschritten wird, von dem das Auslösen der Aktivierungsfunktion abhängt. Im umgekehrten Fall müssten die Gewichte verringert werden, damit die Aktivierungsfunktion nicht feuert. Dieser Prozess wird so lange fortgesetzt, bis das Ergebnis der Vorhersage zufriedenstellend ist (wenn zum Beispiel 95 % der Bilder richtig klassifiziert werden) oder wir einen Punkt erreichen, an dem wir die Ergebnisse auch nach wiederholten Anpassungen der Gewichtungsparameter nicht mehr verbessern können.
Das soeben beschriebene Konzept wird als einschichtiges Perzeptron bezeichnet und stellt die einfachste Version eines neuronalen Netzes dar. Davon gibt es viele Erweiterungen und Varianten, doch bevor wir uns diesen zuwenden, werden wir uns im nächsten Teil dieser Blogserie das einschichtige Perzeptron näher ansehen, wobei uns ein Python-Notebook zur Veranschaulichung dient. Bleiben Sie dran!
Wir danken Tobias Walter für seinen wertvollen Beitrag zu diesem Artikel.